Langues
- English
- Français
Introduction aux mathématiques
- Partie I : Présentation, plan et motivations
- Partie II : Bases de la logique mathématique
- Partie III : Éléments de la théorie des ensembles
- Partie IV : Relations, applications et suites
- Partie V : Domaines majeurs des mathématiques
Partie III : Éléments de la théorie des ensembles
Contents
Contents
1. Introduction
2. Ensembles
3. Sous-ensembles
4. Définition intentionnelle d’ensembles
5. Opérations sur ensembles
6. Ensembles notoires de nombres
7. Récapitulatif
La théorie des ensembles est une théorie mathématiques qui étudie les “ensembles”, leurs propriétés et les opérations que l’on peut leur appliquer. Nous ne prendrons pas une approche axiomatique et nous n’examinerons donc pas les possibles problèmes que soulèvent de tels développements. Nous souhaitons simplement introduire les définitions et les propriétés de base pour lae lecteurice débutant’e.
“Formaliser” signifie définir de manière non ambiguë de nouveaux concepts à partir de définitions préexistantes qui ont a leur tour été soit formalisées soit se trouvent être des “notions primitives” de la théorie. Pour cette raison, la théorie des ensembles est centrale dans les mathématiques. En effet c’est la théorie classique qui sert de cadre pour formaliser toutes les mathématiques. Il est donc d’importance majeure que les éléments de base de la théorie des ensembles soient bien compris pour étudier le reste des mathématiques. Il s’agit de l’objectif de ce document ainsi que du prochain document dans cette série “Introduction aux mathématiques”.
Dans ce document, nous allons parler de la notion primitive d’ensemble, de ce que sont les sous-ensembles, de ce que signifie d’utiliser des définitions intentionnelles d’ensembles. Nous définirons par la suite les opérations de base que l’on peut appliquer aux ensembles et, enfin, nous mentionnerons les ensembles notoires de nombres pour illustrer tout ce que nous aurons introduit jusqu’à ce point.
Les connaissances prérequises pour suivre ce document sont les bases de la logique mathématique notamment les propositions, les connecteurs logiques, les prédicats et les quantificateurs. Ces notions sont introduites dans le document “partie II” de cette série.
Pour une introduction plus poussée mais restant facile à lire (en anglais) de la théorie des ensembles, se référer à [1].
Aucune définition formelle de ce qu’est un ensemble ne peut être donnée : il s’agit d’un concept tellement primitif qu’il n’est pas vraiment possible de le formaliser, c’est-a-dire le définir à partir de notions préexistantes. C’est pour cela que la plupart du temps une définition “intuitive” est donnée plutôt qu’une définition formelle.
Le terme collection est souvent utilisé comme un synonyme d’ensemble. Le mot classe est aussi parfois utilisé de la même manière, cependant il n’est pas recommandé de l’utiliser autant car certains développements de la théorie des ensembles associent un sens bien précis à ce mot. Par convention, une variable désignant un ensemble s’écrit avec une lettre latine majuscule.
Si $A$ est un ensemble, alors les objets mathématiques que $A$ contient sont appelés les éléments de $A$. Si $a$ est un élément de l’ensemble $A$, alors on écrit $a \in A$, ce qui doit se lire “$a$ est dans $A$”, “$a$ est un élément de $A$” ou même “$a$ appartient à $A$”. Le symbole $\in$ représente donc la relation d’appartenance d’un élément avec un ensemble le contenant. Si l’on veut dénoter qu’un objet mathématique $b$ n’appartient pas à l’ensemble $A$ on écrit $b \notin A$.
Comme nous l’avons mentionné dans la partie II, les variables prennent des valeurs prises dans un certain “univers de discours”. Cependant, en pratique cet univers n’est pas explicitement défini et plutôt que les quantificateurs parcourent tout l’univers de discours, on les restreint à des ensembles que l’on donne explicitement. Concrètement, si $P[x]$ est un prédicat (on rappelle que la notation $P[x]$ signifie que si $P$ possède une variable libre alors c’est $x$), plutôt que d’avoir $\forall x, P(x)$, c’est-à-dire faire parcourir la variable $x$ sur tout l’univers de discours, on spécifie un ensemble $A$ qui contiendra les valeurs possibles de $x$ et on écrit : $\forall x \in A, P(x)$. Il faut comprendre cette notation comme une abbréviation pour : \[ (\forall x \in A, P(x)) \overset{\mathrm{def}}{\SSI} (\forall x, x \in A \Rightarrow P(x)) \] Similairement, on définit : \[ (\exists x \in A, P(x)) \overset{\mathrm{def}}{\SSI} (\exists x, x \in A \land P(x)) \] Ici le symbole $\overset{\mathrm{def}}{\Leftrightarrow}$ signifie que le côté gauche de l’équivalence définit une abbréviation pour le côté droit de l’équivalence.
On peut alors montrer que les négations de ces propositions sont données par : \begin{align*} \neg (\forall x \in A, P(x)) &\SSI \neg(\forall x, x \in A \Rightarrow P(x)) && \text{par définition de “$\forall x \in A$”}\\ &\SSI (\forall x, x \notin A \lor \neg P(x)) && \text{puisque $(X \Rightarrow Y) \Leftrightarrow (\neg X \lor Y)$ est une tautologie} \\ &\SSI (\exists x, x \in A \land \neg P(x)) && \text{en prenant la négation: ($\forall \rightarrow \exists$, et lois de De Morgan)} \\ \neg (\forall x \in A, P(x)) &\SSI (\exists x \in A, \neg P(x)) && \text{par définition de “$\exists x \in A$”} \end{align*} et \begin{align*} \neg (\exists x \in A, P(x)) &\SSI \neg(\exists x, x \in A \land P(x)) && \text{par définition de “$\exists x \in A$”} \\ &\SSI (\forall x, x \notin A \lor \neg P(x)) && \text{en prenant la négation: ($\exists \rightarrow \forall$, et lois de De Morgan)} \\ &\SSI (\forall x, x \in A \Rightarrow \neg P(x)) && \text{puisque $(X \Rightarrow Y) \Leftrightarrow (\neg X \lor Y)$ est une tautologie} \\ \neg (\exists x \in A, P(x)) &\SSI (\forall x \in A, \neg P(x)) && \text{par définition de “$\forall x \in A$”} \end{align*}
Si on veut raccourcir une succession de quantificateurs agissant sur des variables parcourant le même ensemble on utilise la notation suivante : \[ \forall x, y \in A, P(x, y) \overset{\mathrm{def}}{\SSI} \forall x \in A, \forall y \in A, P(x, y) \] où $P[x, y]$ est un prédicat.
Dans cet exemple, on utilise que deux variables, mais on le généralise à n’importe quel nombre de variables : \[ \forall \DOTS{x_1, x_2}{x_n} \in A, P(\DOTS{x_1, x_2}{x_n}) \overset{\mathrm{def}}{\SSI} \DOTS{\forall x_1 \in A, \forall x_2 \in A}{\forall x_n \in A}, P(\DOTS{x_1, x_2}{x_n}) \]
Maintenant que nous avons introduit plusieurs notations sur les ensembles, posons-nous la question : comment construire des ensembles ? Pour définir un ensemble, deux façons existent : une définition extensionnelle et une définition intentionnelle. Nous parlerons de cette dernière plus tard dans le document. Pour l’instant, attachons-nous à expliquer ce que signifie la première.
Une définition extensionnelle d’un ensemble $A$ consiste à lister explicitement tous les éléments de l’ensemble $A$. Une manière bien pratique pour cela est d’utiliser la notation de Roster : considèrons l’ensemble $A$ dont les éléments sont les nombres $0$, $2$ et $5$, dans la notation de Roster nous écrivons : \[ A = \ensemble{0, 2, 5} \] Cela consiste à lister les éléments de l’ensemble en les séparant par des virgules et en les entourant d’accolades.
Définir des ensembles consistant d’un nombre fini d’éléments est particulièrement adapté à cette notation, notamment quand il n’y en a que quelques-uns. Cependant, cette notation limite considèrablement les ensembles que l’on peut définir. Une manière de contourner cette limitation est d’ajouter un sens implicit à l’aide des “trois petits points”. Par exemple, si l’on veut définir l’ensemble $B$ comme l’ensemble des nombres entiers entre $1$ et $100$ on pourra écrire : \[ B = \ensemble{\DOTS{1, 2}{100}} \]
Si l’on veut que l’ensemble $C$ contienne tous les nombres entiers à partir de $0$ (il aura donc un nombre infini d’éléments), nous pouvons écrire : \[ C = \ensemble{0, 1, 2, \cdots} \]
De cette manière, on peut définir de nombreux ensembles lorsque les éléments suivent une suite logique qui peut être exprimée en écrivant simplement les premiers éléments. Cela étant dit, il est important de toujours garder à l’esprit que l’utilisation des “trois petits points” apporte un sens implicit qui pourrait être interprété de différentes manières, ce qui est exactement ce que l’on veut éviter en mathématiques. Si jamais il existe un risque de confusion, alors il est conseillé de soit expliquer dans un langage naturel comme le français quels sont les éléments de l’ensemble soit d’utiliser une définition intentionnelle.
Un point important à se souvenir : les ensembles sont complètement déterminés par leurs éléments. Cela signifie que deux ensembles sont égaux si et seulement s’ils consistent d’exactement les mêmes éléments. Formellement, si $A$ et $B$ sont des ensembles, on a : \[ A = B \SSI (\forall x, x \in A \Leftrightarrow x \in B) \]
Cela implique notamment que l’ordre dans lequel les éléments sont présentés dans la notation de Roster ne change pas l’ensemble décrit. Par exemple, on a : \[ \ensemble{0, 2, 5} = \ensemble{5, 0, 2} \]
De plus, les éléments sont uniques dans le sens où un même élément “n’apparait” en réalité qu’une seule fois dans l’ensemble, peu importe le nombre de fois où il apparait dans la notation de Roster. Par exemple, on a : \[ \ensemble{0, 0, 0} = \ensemble{0} \]
Pour dénoter que deux ensembles $A$ et $B$ ne sont pas égaux, on utilise la notation $A \neq B$. Par définition, deux ensembles ne sont pas égaux s’il existe un élément dans l’un qui n’est pas dans l’autre.
Un ensemble notoire est l’ensemble vide, représenté par le symbole $\emptyset$ : c’est l’ensemble qui ne contient aucun élément. Dans la notation de Roster, on a : \[ \emptyset = \ensemble{} \]
Remarquons que pour tout prédicat $P[x]$, la proposition $\exists x \in \emptyset, P(x)$ est toujours fausse car il n’existe aucun élément dans l’ensemble $\emptyset$ et donc aucun élément ne peut satisfaire la proposition. Considérons à présent la proposition $\forall x \in \emptyset, P(x)$. Elle est toujours vraie et pour comprendre pourquoi, réfléchissons à ce que signifierait de la supposer fausse : sa négation est $\exists x \in \emptyset, \neg P(x)$ mais nous venons de dire qu’une proposition qui consiste de $\exists x \in \emptyset$ est toujours fausse. La négation étant fausse implique nécessairement que la proposition originale est vraie. Pour récapituler, une proposition de la forme “$\exists x \in \emptyset, P(x)$” est toujours fausse tandis qu’une proposition de la forme “$\forall x \in \emptyset, P(x)$” est toujours vraie.
On appelle singleton tout ensemble qui consiste d’exactement un élément. Une paire est un ensemble consistant d’exactement deux éléments distincts.
Comme il est souvent de coutume en mathématiques, après avoir défini un nouvel objet, on se questionne s’il est possible “d’extraire” de ce nouvel objet un autre objet qui vérifie des propriétés similaires à l’objet de départ. En termes d’ensembles : peut-on obtenir de nouveaux ensembles “contenus” dans des ensembles préexistants ? La réponse est oui. Puisque les ensembles sont simplement des collections d’éléments, il suffit de prendre quelques éléments de l’ensemble à l’étude pour créer un nouveau ensemble que nous appelerons “sous-ensemble”.
On dénote une telle relation en écrivant $B \subseteq A$ ou, de manière équivalente, $A \supseteq B$.
Formellement, on a : \[ B \subseteq A \overset{\mathrm{def}}{\SSI} \forall x \in B, x \in A \]
Le symbole $\subseteq$ représente la relation d’inclusion. Pour indiquer que $B$ n’est pas un sous-ensemble de $A$, on écrit $B \not\subseteq A$ ou, de manière équivalente, $A \not\supseteq B$.
Par exemple, si l’on considère l’ensemble $A = \ensemble{a, b, c}$ alors les ensembles $\ensemble{a, b}$ et $\ensemble{c}$ sont des exemples de sous-ensembles de $A$.
Remarquons deux relations d’inclusion importantes vérifiées par n’importe quel ensemble : \puce Soit $a \in A$, alors $a \in A$ ce qui signifie par définition que $A \subseteq A$.
Parfois, on souhaite travailler avec des collections de sous-ensembles d’un ensemble $A$ donné. Nous introduisons donc l’ensemble suivant qui contient tous les ensembles de $A$ : L’ensemble des parties de $A$ est la collection de tous les sous-ensembles de $A$. On le dénote par $\Pcal(A)$ ou $2^{A}$. Formellement, on a : \[ X \in \Pcal(A) \overset{\mathrm{def}}{\SSI} X \subseteq A \]
Par exemple, si $A = \ensemble{a, b, c}$ consiste des trois éléments $a$, $b$ et $c$, alors l’ensemble des parties de l’ensemble $A$ est donné par : \[ \Pcal(A) = \ensemble{\emptyset, \ensemble{a}, \ensemble{b}, \ensemble{c}, \ensemble{a, b}, \ensemble{a, c}, \ensemble{b, c}, A} \]
Il est important de bien comprendre que l’ensemble des parties d’un ensemble est un ensemble dont les éléments sont eux-mêmes des ensembles. Remarquons par exemple que $\ensemble{a} \in \Pcal(A)$ mais que a priori $a \notin \Pcal(A)$ : les éléments de $\Pcal(A)$ sont eux-mêmes des ensembles contenant des éléments de l’ensemble original $A$. De plus, remarquons que peu importe l’ensemble $A$ considéré, l’ensemble des parties de $A$ n’est pas vide car il contient au moins l’ensemble vide $\emptyset$.
Il existe des notations pour la relation d’inclusion $\subseteq$ qui sont analogues à celles pour la relation d’appartenance $\in$. Soit $P[X]$ un prédicat et $A$ un ensemble. Alors on introduit les notations :
- pour le quantificateur universel : $\forall X \subseteq A, P(X) \overset{\mathrm{def}}{\SSI} \forall X \in \Pcal(X), P(X)$
- pour le quantificateur existentiel : $\exists X \subseteq A, P(X) \overset{\mathrm{def}}{\SSI} \exists X \in \Pcal(X), P(X)$
À présent mentionnons un théorème très important qui caractérise l’égalité entre ensembles en termes de relations d’inclusion : \puce Commençons par supposer que $A = B$. Par la proposition 3 on a $A \subseteq B$ and $B \subseteq A$. \puce À présent, supposons que $A \subseteq B$ et $B \subseteq A$. Alors si $x$ est un élément de l’univers de dicours, si on suppose que $x \in A$ alors il s’ensuit que $x \in B$ puisque $A \subseteq B$. De manière analogue, si on suppose $x \in B$ alors $x \in A$ par $B \subseteq A$. Donc, on a bien $x \in A \Leftrightarrow x \in B$, pour tout $x$ dans l’univers de discours, ce qui nous permet de conclure que $A = B$. D’où $(A \subseteq B \ET B \subseteq A) \ALORS A = B$
Nous appelerons cette méthode pour montrer l’egalité entre ensembles : double inclusion. En pratique, c’est souvent la méthode que l’on utilise pour montrer que deux ensembles sont égaux.
La seconde relation $A \subseteq A$ de la proposition 3 signifie que la relation d’inclusion est réflexive. Le théorème 5 signifie que la relation d’inclusion est anti-symétrique. Maintenant, la proposition suivante affirme que la relation d’inclusion est transitive. (Ces trois termes seront définis dans un cadre plus général dans la partie IV quand nous parlerons des relations)
Comme présenté dans le théorème 5, deux ensembles sont égaux s’ils vérifient une double inclusion. Parfois cependant, une inclusion peut être satisfaite tandis que l’autre ne le soit pas. Pour indiquer quand c’est le cas, on définit une nouvelle relation appelée inclusion stricte :
Notons que le symbole $\subset$ existe aussi et à première vue pourrait être utilisé pour dénoter la relation d’inclusion stricte. Cependant, en pratique, la plupart des auteurices l’utilise comme un remplaçant au symbole $\subseteq$ et non $\subsetneq$.
4. Définition intentionnelle d’ensembles
Discutons à présent de l’autre manière de définir des ensembles. Une définition intentionnelle d’un ensemble $B$ consiste à spécifier une condition logique qui fera la différence entre objets qui la satisfont (et par conséquent appartiendront à l’ensemble $B$) et ceux qui ne la vérifient pas (et donc ne seront pas des éléments de $B$). Pour éviter des paradoxes possibles qui pourraient intervenir si l’on ne fait pas attention, on se restreindra à l’utilisation de définition intentionnelle aux sous-ensembles d’ensembles préexistants. En d’autres termes, pour définir intentionnellement un ensemble nous avons besoin de la condition logique et du sur-ensemble duquel sont tirés les potentiels éléments de $B$.
On utilise la notation en compréhension pour définir intentionnellement des ensembles. Soit $A$ un ensemble et $P[x]$ un prédicat. On définit alors le sous-ensemble $B$ de l’ensemble $A$ dont les éléments sont exactement les éléments de $A$ qui satisfont le prédicat $P$ ; on écrit alors : \[ B = \ens{x \in A}{P(x)} \] En d’autres termes, on a : \[ \forall x \vir (x \in B \overset{\mathrm{def}}{\SSI} (x \in A \ET P(x))) \]
(Notons que la notation en compréhension agit comme un mutificateur sur la variable $x$. Ainsi, le symbole $x$ peut être remplacé par n’importe quel autre symbole sans affecter le sens, tant que le nouveau symbole n’apparait pas déjà dans l’expression.)
Des notations alternatives préfèrent la virgule “$,$”, le point-virgule “$;$”, les deux points “$:$” ou le slash “$/$” à la barre verticale “$\vert$” mais elles signifient toutes la même chose.
On déduit de la définition ci-avant que pour qu’un élément $x$ de l’univers de discours, on a les équivalences : \[ x \notin B \SSI (x \notin A \lor \neg P(x)) \SSI (x \in A \Rightarrow \neg P(x)) \]
D’autre part, on a $B = A$ si, et seulement si la proposition $P(x)$ est vérifiée pour tout $x \in A$. En particulier, si $P(x)$ est une tautologie pour n’importe quel $x \in A$ alors $A = B$. Au contraire, si $P(x)$ est une antilogie pour tout $x \in A$, alors $B$ est vide.
On appelle le prédicat $P[x]$ la condition d’admissibilité de l’ensemble $B$ : les éléments de $B$ sont exactement les éléments de $A$ qui satisfont la condition d’admissibilité de $B$.
La proposition suivante caractérise la relation d’inclusion en termes des conditions d’admissibilité d’ensembles définis intentionnellement :
Soit $X = \ens{x \in A}{P(x)}$ et $Y = \ens{x \in B}{Q(x)}$. Alors on a : \[ X \subseteq Y \SSI (\forall x \in A, P(x) \Rightarrow (x \in B \land Q(x))) \] \puce Supposons que $\forall x \in A, P(x) \Rightarrow (x \in B \land Q(x))$. Soit $x \in X$. Alors $P(x)$ est vraie. Mais puisque $P(x) \Rightarrow (x \in B \land Q(x))$, par modus ponens il s’ensuit que $x \in B$ et que $Q(x)$ est vraie. Donc $x \in Y$. D’où $X \subseteq Y$.
On retiendra que lorsque deux ensembles sont définis intentionnellement alors la relation d’inclusion entre eux est caractérisée par l’implication logique de leurs conditions d’admissibilité respectives.
Une conséquence de cela est une nouvelle caractérisation de l’égalité des ensembles, quand ils sont définis intentionnellement : Soit $X = \ens{x \in A}{P(x)}$ et $Y = \ens{x \in B}{Q(x)}$. Alors : \[ X = Y \SSI (\forall x, (x \in A \land P(x)) \Leftrightarrow (x \in B \land Q(x))) \] Mais l’on sait que $(M \Rightarrow (N \Rightarrow R)) \Leftrightarrow ((M \land N) \Rightarrow R)$ est une tautologie. Alors $X \subseteq Y \Leftrightarrow (\forall x, (x \in A \land P(x)) \Rightarrow (x \in B \land Q(x)))$. Similairement, on obtient $Y \subseteq X \Leftrightarrow (\forall x, (x \in B \land Q(x)) \Rightarrow (x \in A \land P(x)))$. Donc, par le théorème 5, on a $X = Y \Leftrightarrow (\forall x, (x \in A \land P(x)) \Leftrightarrow (x \in B \land Q(x)))$
Nous avons dit plus tôt dans le document qu’en pratique on utilise généralement une double inclusion pour montrer l’égalité entre deux ensembles. La deuxième façon la plus courante consiste à prouver l’équivalence des conditions d’admissibilité lorsque les ensembles en question ont été définis intentionnellement.
Nous avons à présent la capacité de définir des ensembles de deux manières différentes : au travers d’une définition extensionnelle ou d’une définition intentionnelle. Maintenant, intéressons-nous à d’autres façons de construire de nouveaux ensembles à partir d’ensembles préexistants : par le moyen d’opérations ensemblistes. Il en existe de nombreuses ; nous allons définir les plus importantes, en commençant par la réunion de deux ensembles :
Par exemple, si
- $A := \ensemble{1, 2, 3}$ et $B := \ensemble{4, 5}$ alors $A \cup B = \ensemble{1, 2, 3, 4, 5}$.
- $A := \ensemble{1, 2, 3}$ et $B := \ensemble{3, 4}$ alors $A \cup B = \ensemble{1, 2, 3, 4}$.
- $A$ est un ensemble, alors $A \cup \emptyset = A$.
On peut définir une autre opération ensembliste, appelée intersection de deux ensembles :
Par exemple, si :
- $A := \ensemble{1, 2, 3}$ et $B := \ensemble{4, 5}$ alors $A \cap B = \emptyset$.
- $A := \ensemble{1, 2, 3}$ et $B := \ensemble{3, 4}$ alors $A \cap B = \ensemble{3}$.
- $A$ est un ensemble, alors $A \cap \emptyset = \emptyset$.
Maintenant quelques conséquences élémentaires de définitions de la réunion et l’intersection de deux ensembles :
La troisième de ces équations dans chaque colonne donne un sens aux expressions “$A \cup B \cup C$” et “$A \cap B \cap C$” (remarquons l’absence de parenthèses) puisqu’elles signifient que l’ordre dans lequel les opérations sont appliquées n’impacte pas l’ensemble résultant : cette propriété de $\cup$ et $\cap$ est appelée associativité. Cette propriété se généralise à n’importe quel nombre d’ensembles : ce qui nous permet de définir sans ambiguïtés la réunion et l’intersection d’un nombre arbitraire $n$ d’ensembles $\DOTS{A_1, A_2}{A_n}$ : \begin{align*} \bigcup_{k = 1}^{n} A_k &:= A_1 \cup A_2 \cup \cdots \cup A_n & \bigcap_{k = 1}^{n} A_k &:= A_1 \cap A_2 \cap \cdots \cap A_n \end{align*} (Ici, la notation $:=$ signifie que le membre de gauche de l’égalité est une abbréviation du membre de droite.)
Les opérateurs $\bigcup_{k = 1}^{n}$ et $\bigcap_{k=1}^{n}$ agissent comme des mutificateurs sur la variable $k$. L’expression $\bigcup_{k = 1}^{n} A_k$ est à lire de la manière suivante : “La réunion des ensembles $A_k$ où $k$ va de $1$ jusqu’à $n$” et l’expression $\bigcap_{k = 1}^{n} A_k$ doit être lue de la même façon en remplaçant réunion par intersection.
Similairement, $\forall k \in \ensemble{\DOTS{1}{n}}, x \in A_{k}$ si et seulement si $\bigwedge_{k = 1}^{n} (x \in A_k)$.
Par exemple, si $A_1 := \ensemble{1, 2, 3, 4}$, $A_2 := \ensemble{0, 2, 4}$ et $A_3 := \ensemble{2, 3, 5}$, alors on a : \begin{align*} \bigcup_{k = 1}^{3} A_k &= A_1 \cup A_2 \cup A_3 = \ensemble{0, 1, 2, 3, 4, 5} \\ \bigcap_{k = 1}^{3} A_k &= A_1 \cap A_2 \cap A_3 = \ensemble{2} \end{align*}
Remarquons les inclusions suivantes :
Bien que nous pourrions étudier plus en détails ces opérations plus générales, nous allons préférer énoncer les propriétés pour les définitions initiales de réunion et d’intersection de deux ensembles car ces résultats pourront être facilement généralisés pour un nombre arbitraire d’ensembles, en vertu des propritétés des connecteurs logiques $\land$ et $\lor$ ainsi que de leurs analogues en théorie des ensembles $\cap$ et $\cup$ (et notamment leur propriété d’associativité).
La proposition suivante affirme que la réunion de deux sous-ensembles de $A$ et de $B$ est un sous-ensemble de $A \cup B$ :
La proposition suivante donne une forme explicite de la réunion de deux ensembles définis intentionnellement : Soit $X := \ens{x \in A}{P(x)}$ et $Y := \ens{x \in B}{Q(x)}$. Alors on a : \[ X \cup Y = \ens{x \in (A \cup B)}{(x \in A \land P(x)) \lor (x \in B \land Q(x))} \] Soit $x$ un élément de l’univers de discours. \begin{align*} \text{Par définition :} && x \in (X \cup Y) &\SSI (x \in X \OU x \in Y) \\ \text{Mais, d’une part :} && x \in X &\SSI (x \in A \ET P(x)) \\ \text{D’autre part :} && x \in Y &\SSI (x \in B \ET Q(x)) \\ \text{Par équivalence :} && x \in (X \cup Y) &\SSI ((x \in A \ET P(x)) \OU (x \in B \ET Q(x))) \end{align*}
De manière similaire à ce que l’on a montré pour la réunion, on a la proposition suivante : Soit $X := \ens{x \in A}{P(x)}$ et $Y := \ens{x \in B}{Q(x)}$. Alors on a : \[ X \cap Y = \ens{x \in (A \cap B)}{P(x) \land Q(x)} \] On peut donner une caractérisation de la relation d’inclusion en termes de réunions et d’intersections : \puce Réciproquement, supposons $A \cup B \subseteq A$. Par la proposition 16 on déduit $B \subseteq A \cup B$. Puis par la proposition 6 on conclut que $B \subseteq A$. \puce Supposons $B \subseteq A$. Soit $x \in B$. Alors par hypothèse, $x \in A$. Donc $x$ est à la fois dans $A$ et dans $B$ ce qui signifie par définition $x \in A \cap B$. Donc on a bien $B \subseteq A \cap B$. \puce Réciproquement, supposons $B \subseteq A \cap B$. De la proposition 16 on déduit $A \cap B \subseteq A$. Enfin, par la proposition 6 on a $B \subseteq A$. Remarquons que, puisque les inclusions $A \subseteq A \cup B$ et $A \cap B \subseteq B$ sont vérifiées pour n’importe quels ensembles $A$ et $B$ comme énoncé dans la proposition 16, nous n’avons pas besoin de rajouter quoique ce soit pour affirmer que les équivalences suivantes sont satisfaites : \[ B \subseteq A \SSI A = A \cup B \SSI B = A \cap B \] Un cas particulier important pour l’intersection de deux ensembles est donné comme suit : En d’autres termes, ils sont disjoints s’ils ne partagent aucun élément en commun. Jusque là nous avons parlé des deux opérations ensemblistes : la réunion et l’intersection. À travers leurs propriétés que nous avons listées, on est arrivé à la conclusion que la réunion ensembliste était analogue à la disjonction logique tandis que l’intersection ensembliste est analogue à la conjonction logique. Nous avons également vu que la relation d’inclusion ensembliste ressemble sous certains aspects à l’implication logique et que l’égalité entre ensembles comportent des similitudes avec l’équivalence logique. Il ne reste plus que la négation logique à laquelle nous n’avons pas encore associé de notion ensembliste. Avec cet objectif en tête, nous introduisons une nouvelle opération qui s’applique sur deux ensembles : En d’autres termes, les éléments de $B \setminus A$ sont exactement les éléments de $B$ qui ne sont pas dans $A$. Par exemple, si : Montrons à présent ce qui relie le complémentaire relatif à la négation logique en termes d’ensembles intentionnellement définis : Soit $X := \ens{x \in A}{P(x)}$ et $Y := \ens{x \in B}{Q(x)}$. Alors on a : \[ Y \setminus X = \ens{x \in Y}{x \in A \Rightarrow \neg P(x)} \] On voit encore mieux le lien avec la négation logique dans le corollaire suivant : À présent, attachons-nous à établir des propriétés de bases du complémentaire relatif. $\emptyset \setminus A = \ens{x \in \emptyset}{x \notin A} = \emptyset$ car il n’existe aucun élément dans $\emptyset$ que l’on pourrait tirer. Voici encore une nouvelle caractérisation de la relation d’inclusion en termes de complémentaire relatif: En particulier, $A \setminus A = \emptyset$. En particulier : $C \setminus (C \setminus A) = C \cap A$. Le cas particulier est déduit de manière directe du cas particulier de la proposition 28. Dans la partie II, nous avons introduit les lois de De Morgan pour la disjonction et la conjonction logiques lorsque l’on considère leur négation. On peut établir des lois analogues pour la réunion et l’intersection ensemblistes par rapport au complémentaire relatif : Réciproquement, nous donnons à présent les équations du compémentaire relatif de n’importe quel ensemble $B$ dans un ensemble exprimé sous la forme d’une réunion ou d’une intersection finie d’ensembles: La démonstration est la même pour l’autre égalité en intervertissant les $\bigcup$ par $\bigcap$ et $\exists$ par $\forall$. \end{proof} En général, l’univers de discours n’est pas un ensemble strictement parlant. Cependant, il advient parfois qu’il s’agit bien d’un ensemble : alors n’importe quel ensemble à notre disposition est un sous-ensemble de cet ensemble. Cela nous permet de définir un autre type de complémentaire (qui est en réalité un cas particulier du complémentaire relatif) : On définit le complémentaire absolu de $A$, ou simplement le complémentaire de $A$, noté $A^{c}$ ou parfois $\ol{A}$, comme l’ensemble des éléments de $U$ qui ne sont pas dans $A$. Formellement, on a : \[ A^{c} := U \setminus A \] Tous les résultats donnés pour le complémentaire relatif s’appliquent également pour le complémentaire absolu. Quelques résultats spécifiques au complémentaire absolu sont donnés ici : Similairement, $(A \cap B)^{c} = U \setminus (A \cap B) = (U \setminus A) \cup (U \setminus B) = A^{c} \cup B^{c}$. Exercice : Montrer que, si $A$, $B$ et $C$ sont des ensembles, alors : \begin{align*} (A \setminus B) \setminus C &= (A \setminus C) \setminus (B \setminus C) & A \text{ et } B \text{ sont disjoints} &\SSI A \setminus B = A \end{align*} Jusque là nous avons étudier des ensembles, c’est-à-dire des collections sans ordre particulier d’éléments uniques (possiblement avec une infinité d’éléments). Nous voudrions à présent introduire un nouvel objet mathématique : les $n$-uplets. Il faut les comprendre comme étant des collections finies et ordonnées d’éléments (qui, possiblement, peut avoir plusieurs le même élément). Pour définir des $n$-uplets de longueur arbitraire, nous introduisons la notion de couple pour pouvoir géneraliser par la suite : Le couple formé des deux éléments $a$ et $b$, que l’on note $(a, b)$, est l’objet mathématique vérifiant la propriété suivante : \[ \forall c \in A \vir \forall d \in B \vir (a, b) = (c, d) \SSI (a = c) \land (b = d) \] Les éléments $a$ et $b$ sont appelés respectivement première et seconde composantes (ou coordonnées). Nous pourrions formaliser cette nouvelle notion à l’aide de concepts ensemblistes que nous avons introduit au préalable mais cela n’apporte pas grand chose dans le contexte de ce document. Nous préférerions que lae lecteurice se souvienne de la propriété précédente qui stipule que deux couples sont égaux si et seulement si leurs première et seconde composantes sont égales. L’ensemble de tous les couples pour des ensembles donnés se définit comme une opération ensembliste: Par exemple, si $A := \ensemble{1, 2}$ et $B := \ensemble{3, 4, 5}$, alors : \[ A \times B = \ensemble{(1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)} \] Une distinction importante entre le produit cartésien de deux ensembles et la réunion ou l’intersection est l’absence d’associativité : pour trois ensembles $A$, $B$ et $C$ donnés, les ensembles $(A \times B) \times C$ et $A \times (B \times C)$ sont a priori différents. Par exemple : $A := \ensemble{1, 2}$, $B := \ensemble{3, 4}$ et $C := \ensemble{5, 6}$, alors $((1, 3), 5)$ est un élément de $(A \times B) \times C$ : il s’agit d’un couple dont la première composante est un couple et la seconde composante est un nombre. Tandis que $(1, (3, 5))$ est un élément de $A \times (B \times C)$ mais c’est un couple dont la première composante est cette fois un nombre et dont la deuxième composante est un couple. En exhibant ces élément, on montre que l’ordre dans lequel se fait les opérations de produit cartésien à un impact sur l’ensemble résultant. C’est en clair contraste avec l’intersection et la réunion de deux ensembles. C’est pour cela que si l’on souhaite généraliser le produit cartésien à un nombre arbitraire d’ensembles nous devons définir explicitement sans avoir recours au produit cartésien sur deux ensembles. Pour cela, commençons par généraliser l’idée de collection finie ordonnée d’éléments à un nombre $n$ quelconque d’éléments Le $n$-uplet formé par les éléments $\DOTS{a_1, a_2}{a_n}$, que l’on note $(\DOTS{a_1, a_2}{a_n})$, est l’objet mathématique vérifiant la propriété suivante : \[ \DOTS[\vir]{\forall b_1 \in A_1\vir \forall b_2 \in A_2}{\forall b_n \in A_n} \] \[ (\DOTS{a_1, a_2}{a_n}) = (\DOTS{b_1, b_2}{b_n}) \SSI \forall i \in \ensemble{\DOTS{1}{n}}, a_i = b_i \] L’élément $a_k$ est appelé $k$-ième composante (ou coordonnée) du $n$-uplet. Remarquons que l’on pourrait formaliser ces nouveaux objets en utilisant les couples ou d’autres notions ensemblistes mais, encore une fois, cela n’aurait pas de grand intérêt en considérant l’objectif de ce document. Notons de plus que, pour $n = 2$, on retombe sur la définition de couple. Un $n$-uplet où $n = 3$ est appelé triplet. où $n = 4$ est appelé quadruplet, etc. Maintenant, définissons le produit cartésien d’un nombre arbitraire d’ensembles : Le produit cartésien de $\DOTS{A_1, A_2}{A_n}$, noté $\DOTS[\times]{A_1 \times A_2}{A_n}$, est l’ensemble consistant de tous les $n$-uplets pour lesquels la $k$-ième composante est dans $A_k$. Formellement : \[ x \in (\DOTS[\times]{A_1 \times A_2}{A_n}) \overset{\mathrm{def}}{\SSI} \DOTS{\exists a_1 \in A_1, \exists a_2 \in A_2}{\exists a_n \in A_n}, x = (\DOTS{a_1, a_2}{a_n}) \] On écrit également : $\displaystyle \prod_{k = 1}^{n} A_k := \DOTS[\times]{A_1 \times A_2}{A_n}$. Notons que la notation $\prod_{k = 1}^{n} A_k$ (lire “le produit cartésien des ensembles $A_k$ où $k$ va de $1$ à $n$”) agit comme un mutificateur sur la variable $k$. Voici un exemple de produit cartésien de trois ensembles. Si $A := \ensemble{1,2}$, $B := \ensemble{3, 4}$ et $C := \ensemble{5, 6}$ : \[ A \times B \times C = \ensemble{(1, 3, 5), (1, 3, 6), (1, 4, 5), (1, 4, 6), (2, 3, 5), (2, 3, 6), (2, 4, 5), (2, 4, 6)} \] Une notation spécifique pour le cas où les $A_k$ sont égaux à un même ensemble $A$. Soit $A$ un ensemble et $n$ un nombre naturel, alors on pose : \[ A^{n} := \prod_{k = 1}^{n} A \] En reprenant l’exemple $A := \ensemble{1, 2}$, on a : \[ A^3 = \ensemble{(1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2)} \] Exercice : Montrer que, si $A$, $B$ et $C$ sont des ensembles, alors : \begin{align*} (A \cap B) \times C &= (A \times C) \cap (B \times C) & (A \setminus B) \times C &= (A \times C) \setminus (B \times C) \end{align*} Pour récapituler, nous avons parlé de comment définir des ensembles et comment en construire de nouveaux à partir d’ensembles préexistants à l’aide d’opérations ensembliste comme la réunion, l’intersection, les complémentaires et le produit cartésien. 6. Ensembles notoires de nombres
Les ensembles les plus connus sont bien évidemment les ensemble de nombres. On souhaite ici les introduire sans les construire formellement, ce qui dépasserait le cadre de ce document. On peut distinguer plusieurs types de nombres différents : en commençant par les entiers naturels. Il s’agit des nombres les plus simples : on les utilise pour compter des choses. L’ensemble de tous les entiers naturels s’écrit $\N$. On a : \[ \N := \ensemble{0, 1, 2, \cdots} \] C’est souvent que l’on veut excluer le cas où une variable qui parcourt un ensemble de nombres prend la valeur $0$. Pour cela, on introduit la notation suivante : \[ \NnonNul := \N \setminus \ensemble{0} \] Si l’on veut considérer en plus les “entiers négatifs”, on s’intéresse alors à l’ensemble des entiers relatifs, noté $\Z$ : \[ \Z := \ensemble{\cdots, -2, -1, 0, 1, 2, \cdots} \] De même que pour les entiers naturels, si l’on veut exclupre $0$, on écrit : \[ \ZnonNul := \Z \setminus \ensemble{0} \] Remarquons que l’ensemble des entiers naturels $\N$ est un sous-ensemble de l’ensemble des entiers relatifs $\Z$. En fait, $\Z$ est exactement la réunion de $\N$ et de l’ensemble des “symétriques additifs” des entiers relatifs. Un symétrique additif d’un entier naturel $n \in \N$ est un entier relatif $m \in Z$ tel que $n + m = 0$. On écrit généralement $-n := m$. Dans $\Z$ on peut effectuer sans problème des additions, des soustractions et des multiplications, cependant on ne peut pas diviser comme on le souhaite. Pour se donner cette capacité on introduit l’ensemble $\Q$ des nombres rationnels qui consiste des fractions d’entiers relatifs. Un élément de $x \in \Q$ est représenté par par deux entiers relatifs $n \in \Z$ et $m \in \ZnonNul$ tel que $x = \frac{n}{m}$. Formellement : \[ x \in \Q \overset{\mathrm{def}}{\SSI} \exists n \in \Z, \exists m \in \ZnonNul, x = \frac{n}{m} \] L’entier $n$ est appelé numérateur tandis que l’entier $m$ est appelé dénominateur. Remarquons que $\Z$ est un sous-ensemble de $Q$ puisque n’importe quel entier relatif $n$ peut s’écrire comme la fraction $\frac{n}{1}$. On aurait pu choisir $\NnonNul$ pour notre dénominateur car $\frac{n}{-m} = \frac{-n}{m}$. On pourrait interpréter l’ensembles $\Q$ comme le produit cartésien de $\Z \times \NnonNul$. Cependant, il faut se rappeler que deux fractions $\frac{n_1}{m_1}$ et $\frac{n_2}{m_2}$ peuvent être égales même quand $n_1 \neq n_2$ et $m_1 \neq m_2$. Ainsi, le produit cartésien $\Z \times \NnonNul$ est en ce sens “trop grand” pour représenter $\Q$. On aurait besoin d’ajouter une contrainte telle que, par exemple, $n$ et $m$ sont premiers entre eux. Mais on ne se soucie pas ici de la construction formelle. Encore une fois on introduit la notation : \[ \QnonNul := \Q \setminus \ensemble{0} \] Les nombres peuvent s’écrire dans une base, par exemple la base $10$ : cela signifie que l’on représente un nombre par une succession de chiffres de $0$ à $9$. Par exemple, les nombres $3$, $42$, $-5$ et $-78$ sont des entiers relatifs exprimés en base $10$. Pour écrire des nombres rationnels en base $10$, il est, la plupart du temps, nécessaire d’introduire un séparateur décimal qui permet à la quantité que l’on souhaite représenter de ne pas être un nombre entier. Par exemple : $\frac{1}{2} = 0,5$, $-\frac{7}{5} = -1,4$ ou encore $\frac{1}{3} = 0,33333\cdots$. Ce dernier exemple montre que les chiffres après la virgule peuvent potentiellement continuer indéfiniment. Cependant, il peut être démontré que les nombres rationnels sont exactement les nombres qui ont : soit une écriture en base $10$ finie, soit une écriture en base $10$ dont les chiffres après la virgule continuent indéfiniment mais suivent un motif répété à l’infini (par exemple, $\frac{9}{44} = 0.20454545\cdots$). Cela laisse de côté les nombres dont l’écriture décimale continue indéfiniment mais aucun motif ne se répète à l’infini dans son développement décimal. On appelle ces nombres : nombres irrationnels. Par exemple, $\sqrt{2}$, $\pi$ et $\E$ sont des nombres irrationnels. On définit l’ensemble des nombres réels, noté $\R$, comme la réunion de l’ensemble des nombres rationnels avec l’ensemble des nombres irrationnels. En d’autres termes, $\R$ est l’ensemble des nombres qui peuvent s’écrire dans une base $10$ tels que leur développement décimal peut être fini ou infini, se répéter à l’infini ou non. On introduit les notations suivantes : \begin{align*} \RnonNul &:= \R \setminus \ensemble{0} & \Rpos &:= \ens{x \in \R}{x \geq 0} & \Rneg &:= \ens{x \in \R}{x \leq 0} \\ & & \RposStrict &:= \ens{x \in \R}{x > 0} & \RnegStrict &:= \ens{x \in \R}{x < 0} \end{align*} Les nombres réels peuvent se représenter géométriquement par la droite réelle : c’est une droite sur laquelle on fixe le nombre $0$ à un endroit et, pour chaque point sur cette droite, la distance entre le point et $0$ est un nombre réel et, réciproquement, tout nombre réel peut être associé à exactement un point de la droite. Remarquons que l’on a les relations d’inclusion suivantes : \[ \N \subsetneq \Z \subsetneq \Q \subsetneq \R \] Dans ce document, nous avons introduit de nombreuses notions. Voici les plus importantes :
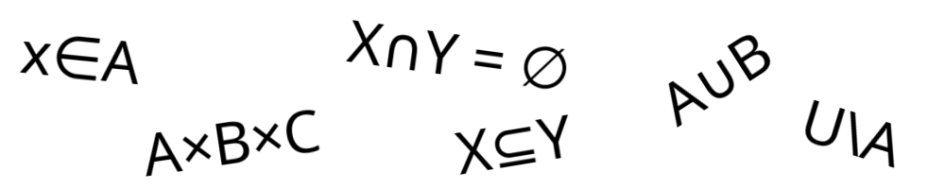
Laisser un commentaire